在上一篇文章中引入条件期望这一概念时,我曾提到:在某些情况下,仅通过期望值信息,我们就能够给出随机过程的一些重要结构性细节。在这篇文章中,我将通过鞅论对这一论断进行进一步阐述。
When introducing the concept of conditional expectations in the previous post, I mentioned that in some cases, “knowing the expected values alone is enough to provide many important structural details of the stochastic process”. In this post, I will further illustrate this idea with the theory of martingales.
鞅的定义 Definition of Martingales
首先,我将给出(离散)鞅的严格定义。一个适应于(离散)滤子$\{\mathcal{F}_n\}$的鞅是一列满足下列条件的一维实值随机变量$\{X_n\}$:
First, I will introduce the formal definition of (discrete) martingales. A martingale adapted to the (discrete) filtration $\{\mathcal{F}_n\}$ is a sequence of one-dimensional real-valued random variables $\{X_n\}$ that satisfies the following conditions:
$$(1) \ E|X_n| < \infty; (2) \ X_n \in \mathcal{F}_n, \ \forall n \in \mathbb{N}; (3) \ E(X_{n+1}|\mathcal{F}_n) = X_n,\text{a.s.}, \ \forall n \in \mathbb{N}. \tag{1.1}$$
在上述定义中,条件(3)是鞅的核心性质:在已有信息$\mathcal{F}_n$的情况下,$X_n$正好给出了对$X_{n+1}$的无偏估计。余下两个条件都是正则性条件:条件(1)要求每个随机变量$X_n$都是可积的(如果不可积,条件(3)就没有意义),而条件(2)要求每个随机变量$X_n$都是相对信息$\mathcal{F}_n$可测的(根据条件期望的定义,这一条件实际上已经隐含在条件(3)中了)。
In the above definition, condition (3) is the core property of martingales: $X_n$ is exactly the unbiased estimate of $X_{n+1}$ given information $\mathcal{F}_n$. The remaining two conditions are for regularities: condition (1) requires that each random variable $X_n$ is integrable (otherwise, condition (3) will be meaningless), while condition (2) requires that each random variable $X_n$ is measurable w.r.t. information $\mathcal{F}_n$ (this condition is implicitly required in condition (3) by the definition of conditional expectations).
通过将条件(3)中的等式“$=$”调整为不小于“$\geq$”或不大于“$\leq$”关系,我们可以进一步定义下鞅或上鞅。换句话说,对于下鞅,随着$n$的增大,条件期望值会单调上升;而对于上鞅,条件期望值会单调下降。
By replacing the equality relationship “$=$” in condition (3) to “$\geq$” or “$\leq$”, we obtain the definition of submartingales or supermartingales. In other words, for submartingales, the conditional expectation increases monotonically as the $n$ increases; while for supermartingales, the conditional expectation decreases monotonically.
下面的图应该能够很直观地对上述定义进行解释:随着时间$n$的推移,鞅序列中的随机变量在经受某种条件期望的反操作。换句话说,$X_{n+1}$相当于在$X_n$的基础上加上一个对于任一可能事件$A\in \mathcal{F}_n$都无偏的随机扰动。
The following figure should provide an intuitive explanation to the above definition: as time $n$ goes in the positive direction, the r.v.s in the martingale sequence are subject to some inverse operations of taking conditional expectations. in other words, $X_{n+1}$ can be viewed as the sum of $X_n$ and a random perturbation which is unbiased for each possible event $A\in \mathcal{F}_n$.
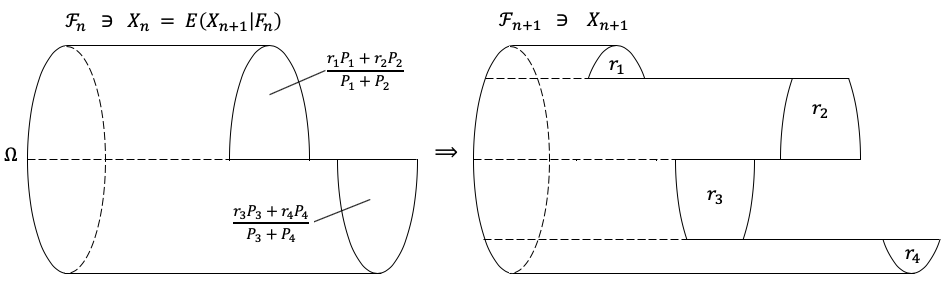
基于上图这种解释,我们可以很容易理解倒鞅的概念。倒鞅即鞅在时间上的倒转,具体来说应满足以下条件:
We can easily understand the concept of backward martingales according to the above discussions. Backward martingales are the reversal of martingales in time, and should satisfy the following condition:
$$X_{n+1} = E(X_n|\mathcal{F}_{n+1}), \ \forall n \in \mathbb{N}, \tag{1.2}$$
其中信息序列$\{\mathcal{F}_{n}\}$满足$\mathcal{F}_0 \supseteq \mathcal{F}_1 \supseteq \cdots \supseteq \mathcal{F}_n \supseteq \cdots$。换句话说,在倒鞅序列中,通过条件期望操作,随机变量在持续被投影到更粗粒度的信息集上;因此,随着$n$的增大,$X_n$会变得越来越“平坦”,并最终收敛到$E(X_0|\mathcal{F}_{\infty})$。而且,很容易证明这种收敛满足a.s.,$L^1$,$L^p$等收敛性质。倒鞅的这种收敛性质可以被用来证明很多强大的结果;下面将给出一个简单的例子。
where the information sequence $\{\mathcal{F}_{n}\}$ satisfies $\mathcal{F}_0 \supseteq \mathcal{F}_1 \supseteq \cdots \supseteq \mathcal{F}_n \supseteq \cdots$. In other words, in a backward martingale, the r.v.s are projected on coarser-grained sets of information by taking conditional expectations. Therefore, as $n$ increases, $X_n$ becomes more “flat” and eventually converges to $E(X_0|\mathcal{F}_{\infty})$. Moreover, it is easy to prove that this convergence is in a.s., $L^1$, and $L^p$. This property of convergence can be used to prove many powerful results; below, I will give a simple example on this point.
假设我们有一列满足$E|X_n|<\infty$的服从独立同分布的随机变量$\{X_n\}$,并令信息$\mathcal{F}_n$为$\sigma(S_n,X_{n+1},\cdots)$;容易看出$\mathcal{F}_0 \supseteq \mathcal{F}_1 \supseteq \cdots \supseteq \mathcal{F}_n$。现在考虑序列和$S_n=\sum_{i=1}^n X_i$。根据$X_n$之间的独立性和对称性,容易证明下式成立:
Suppose we have a sequence of i.i.d. r.v. $\{X_n\}$ that satisfies $\forall n, \ E|X_n|<\infty$. Let information $\mathcal{F}_n$ be $\sigma(S_n,X_{n+1},\cdots)$; it’s obvious that $\mathcal{F}_0 \supseteq \mathcal{F}_1 \supseteq \cdots \supseteq \mathcal{F}_n$. Now let’s consider sums of sequences $S_n=\sum_{i=1}^n X_i$. It is not hard to show, according to the independence and the symmetry among $X_n$, that
$$E(\frac{S_n}{n}|\mathcal{F}_{n+1}) = \frac{1}{n}E(S_n|S_{n+1}) = \frac{1}{n} \cdot \frac{n}{n+1}S_{n+1} = \frac{1}{n+1}S_{n+1}.$$
因此,随机变量序列$\{S_n/n\}$是适应于滤子$\{\mathcal{F}_n\}$的一个倒鞅,从而可根据倒鞅的性质得到强大数定律:
Therefore, the r.v. sequence $\{S_n/n\}$ is a backward martingale adapted to filtration $\{\mathcal{F}_n\}$, and according to properties of backward martingales we can derive the following strong law of large numbers:
$$\lim_{n} \frac{S_n}{n} = E(X_1|\mathcal{F}_{\infty}) = EX_1, \ a.s.$$
(注:第二个等式的证明需要使用Hewitt-Savage 0-1律来证明$\mathcal{F}_{\infty}$是不含任何信息的,即对任意$A \in \mathcal{F}_{\infty}$,有$P(A) \in \{0,1\}$;这里暂时不做详细讨论。)
(Note: To prove the second equation, one needs to use the Hewitt-Savage 0-1 law to show that $\mathcal{F}_{\infty}$ is trivial, i.e., for any $A \in \mathcal {F}_{\infty}$, $P(A) \in \{0,1\}$; I won’t discuss this 0-1 law in details here.)
理论性质 Theoretical Properties
在这一节中,我将介绍一些鞅的理论性质。为简便起见,我将直接用$X_n$表示鞅、$\mathcal{F}_n$表示滤子,以代替序列写法$\{X_n\}$和$\{\mathcal{F}_n\}$。
In this section, I will introduce some theoretical properties of martingales. For the sake of brevity, I will use $X_n$ for martingales and $\mathcal{F}_n$ for filtrations, instead of $\{X_n\}$ and $\{\mathcal{F}_n\}$.
基本性质 Basics
在这一小节中,我将讨论鞅的性质在哪些映射变换下能够保持不变,并利用这种不变性推导一些有用的结果。首先,容易看出仿射变换是保持鞅性质的。
In this subsection, I will discuss under which kinds of mappings martingale properties are preserved, and use such invariances to derive several useful results. First, it is easy to see that affine transformations preserve the martingale property.
定理2.1:若$X_n,Y_n$是两个次/上鞅,则$X_n+Y_n$是一个次/上鞅;若$X_n$是一个次/上鞅,那么对于任意$c \in \mathbb{R}^+$,$cX_n$也是一个次/上鞅。
Theorem 2.1: If $X_n, Y_n$ are two sub/supermartingales, then $X_n+Y_n$ is a sub/supermartingale; if $X_n$ is a sub/supermartingale, then for any $c \in \mathbb{R}^+$, $cX_n$ is also a sub/supermartingale.
对于一般的非线性变换,要保持鞅性是比较困难的;但我们可以退一步,通过不等式关系来保持次/上鞅的性质:
For general nonlinear transformations, it is more difficult to preserve the martingale property; but we can step back and keep the sub/supermartingale property via inequalities:
定理2.2:假设$\varphi$是一个凸函数。若鞅$X_n$满足$E|\varphi(X_n)|<\infty, \ \forall n \in \mathbb{N}$,则根据琴生不等式,有
Theorem 2.2: Suppose $\varphi$ is a convex function. If $X_n$ is a martingale with $E|\varphi(X_n)|<\infty, \ \forall n \in \mathbb{N}$, then according to Jensen’s inequality, we have
$$E(\varphi(X_{n+1})|\mathcal{F}_n)\geq \varphi(E(X_{n+1}|\mathcal{F}_n)) = \varphi(X_{n}); \tag{2.1.1}$$
即$\varphi(X_n)$是一个下鞅。进一步地,若函数$\varphi$是单调递增的,那么按照式(2.1.1)中的推导,容易证明对一个下鞅$X_n$,$\varphi(X_n)$也是一个下鞅。
that is, $\varphi(X_n)$ is a submartingale. Moreover, if the function $\varphi$ is monotonically increasing, then it is easy to show, following the derivation in equations (2.1.1), that for a submartingale $X_n$, $\varphi(X_n)$ is also a submartingale.
根据定理2.2,可以推导出以下结论:
推论2.2.1:若$X_n$是一个鞅,且有$p \geq 1$满足$E|X_n|^p<\infty, \ \forall n \in \mathbb{N}$,则$X_n^p$是一个下鞅。
推论2.2.2:若$X_n$是一个下鞅,那么对于任意$a \in \mathbb{R}$,$(X_n - a)^+$也是一个下鞅。
推论2.2.3:若$X_n$是一个下鞅,那么对于任意$a \in \mathbb{R}$,$X_n \vee a$也是一个下鞅。
We can derive the following corollaries from theorem 2.2:
Corollary 2.2.1: If $X_n$ is a martingale, and there is a $p \geq 1$ such that $E|X_n|^p<\infty, \ \forall n \in \mathbb{N}$, then $X_n^p$ is a submartingale.
Corollary 2.2.2: If $X_n$ is a submartingale, then for any $a \in \mathbb{R}$, $(X_n - a)^+$ is also a submartingale.
Corollary 2.2.3: If $X_n$ is a submartingale, then for any $a \in \mathbb{R}$, $X_n \vee a$ is also a submartingale.
最后,让我们考虑一种特殊的变换。
Finally, let’s consider a special mapping.
定理2.3:假设有一列适应于滤子$\mathcal{F}_n$的可预测的随机变量$H_n$,即$H_{n+1} \in \mathcal{F}_{n}, \ \forall n \in \mathbb{N}$。根据条件期望的性质,有
Theorem 2.3: Suppose there is a sequence of predictable random variable $H_n$ adapted to filtrations $\mathcal{F}_n$, i.e., $H_{n+1} \in \mathcal{F}_{n}, \ \forall n \in \mathbb{N}$. From the properties of conditional expectations, we have
$$E(\sum_{i=1}^{n+1}H_i(X_i - X_{i-1})|\mathcal{F}_n) = \sum_{i=1}^{n}H_i(X_i - X_{i-1}) + H_{n+1}(E(X_{n+1}|\mathcal{F}_n) - X_{n}); \tag{2.1.2}$$
因此,若$X_n$是一个次/上鞅,且$H_n$非负有界,则可知$(H\cdot X)_n \equiv \sum_{i=1}^{n}H_i(X_i - X_{i-1})$也是一个次/上鞅。特别地,若$X_n$是一个鞅,则$(H\cdot X)_n$也是一个鞅(此处不要求$H_n$的非负性)。
Therefore, if $X_n$ is a sub/supermartingale, and $H_n$ is non-negative and bounded, then $(H\cdot X)_n \equiv \sum_{i=1}^{n} H_i(X_i - X_{i-1})$ is also a sub/supermartingale. In particular, if $X_n$ is a martingale, then $(H\cdot X)_n$ is also a martingale (the non-negative requirement of $H_n$ can be dropped here).
如果我们将上面的$X_n$看作是某种资产在不同时期的价格,而$H_n$看作是“投资决策”,则可预测性$H_{n+1} \in \mathcal{F}_{n}$表明$n+1$时刻的决策是仅根据$n$时刻已有的信息所作出的,即决策者没有依赖未来的信息。在这种情况下,定理2.3说明,如果$X_n$是一个鞅,那么无论决策者如何努力(利用已有信息进行决策),其预期的增量收益都是0。
If we regard the $X_n$ above as the prices of an asset at different times, and $H_n$ as “investment decisions”, then the predictability $H_{n+1} \in \mathcal{F}_{n}$ requires that the decision at time $n+1$ is made w.r.t. the information available at time $n$ and only at time $n$; in other words, the decision maker does not rely on any future information. In this case, theorem 2.3 says that if $X_n$ is a martingale, then no matter how hard the decision maker works (in exploiting existing information), her expected gain is zero.
下面两个例子说明,通过构造合理的$H_n$,可以使用定理2.3获得很有意思的结论。
The next two examples show that by constructing appropriate $H_n$, one can derive interesting results from theorem 2.3.
推论2.3.1:假设$X_n$是一个下鞅,$T$是一个$\mathcal{F}$可测的停时。若令$H_n = 1_{\{T\geq n\}}$,则容易看出$H_n$是可预测、且非负有界的。因此,根据定理2.3,$(H\cdot X)_n=X_{T \wedge n} - X_0$是一个下鞅。
Corollary 2.3.1: Suppose $X_n$ is a submartingale, and $T$ is a $\mathcal{F}$-measurable stopping time. If we let $H_n = 1_{\{T\geq n\}}$, it is easy to show that $H_n$ is predictable, non-negative, and bounded. Therefore, according to the theorem 2.3, $(H\cdot X)_n=X_{T \wedge n} - X_0$ is a submartingale.
推论2.3.2(上穿不等式):假设$X_n$是一个下鞅,$a<b$是两个给定的实数。令$H_n$定义如下:$H_n \in \{0,1\}$,且$H_n = 1$当且仅当在历史序列$X_0,\cdots,X_{n-1}$中,最近一次满足$X_{n} \leq a$的时间要晚于最近一次满足$X_{n} \geq b$的时间。换句话说,每当$X_{n}$的取值降到$a$或以下时,$H_n$的取值会变成1;而当$X_{n}$的取值上升到$b$或以上时,$H_n$的取值会变为0。因此,每一段$H_n$连续取值为1的情形都对应了一次$X_{n}$的取值从$\leq a$“上穿”到$\geq b$的情形。如果定义$U_n$为所有这种情况的发生次数,那么容易看出
Corollary 2.3.2 (Upcrossing inequality): Suppose $X_n$ is a submartingale, $a<b$ are two real numbers. Let $H_n$ be defined as follows: $H_n \in \{0,1\}$, and $H_n = 1$ if and only if in the historical sequence $X_0, \cdots, X_{n-1}$, the last occurrence of $X_{n} \leq a$ happened later than the last occurrence of $X_{n} \geq b$. In other words, whenever the value of $X_{n}$ falls below $a$, we set $H_n = 1$, and whenever the value of $X_{n}$ rises above $b$, $H_n = 0$. Therefore, each occurrence of consecutive events $\{H_n = 1\}$ corresponds to a case that $X_{n}$ “upcross” from $\leq a$ to $\geq b$. If we further define $U_n$ as the number of occurrences of such upcrossing, it is obvious that
$$(b-a)U_n \leq (H\cdot Y)_n,$$
其中$Y_n = X_n \vee a$。(注:为何上式中需要$Y_n$,而不是直接考虑$X_n$?)
where $Y_n = X_n \vee a$. (Note: Why do we need $Y_n$ instead of $X_n$ in above?)
现在,根据推论2.2.3,可知$Y_n$也是一个下鞅。然后,注意到$K_n \equiv 1 - H_n$也是可预测的,故根据定理2.3可知
Now, according to corollary 2.2.3, $Y_n$ is also a submartingale. Also notice that $K_n \equiv 1 - H_n$ is predictable. So according to theorem 2.3,
$$Y_n - Y_0 = (H\cdot Y)_n + (K\cdot Y)_n \geq (H\cdot Y)_n + (K\cdot Y)_0 = (H\cdot Y)_n.$$
将以上两个不等式整合,再取期望,即有
Combining the above two inequalities and then taking expectations, we have
$$(b-a)EU_n \leq E(X_n - a)^+ - E(X_0 - a)^+. \tag{2.1.3}$$
收敛性 Convergence
鞅的一个重要性质是具有很好的收敛性。在这一小节中,我将介绍一些基础的收敛性结果。
An important property of martingales is that they have some nice convergence properties. In this subsection, I will introduce several basic results on this topic.
首先,我们考虑几乎处处(almost surely, a.s.)的逐点收敛:该收敛要求对几乎每个样本$\omega \in \Omega$,实值序列$X_n(\omega)$都是收敛的。换句话说,a.s.-收敛对应以下条件:
First, let’s consider the almost surely (a.s.) convergence, which requires that the real-valued sequence $X_n(\omega)$ is convergent for almost every sample $\omega \in \Omega$. In other words, the a.s. convergence is equivalent to the following condition:
$$P(\{\omega:\liminf_n X_n(\omega) < \limsup_n X_n(\omega)\}) = 0. \tag{2.2.1}$$
注意到
Notice that
$$\begin{aligned} & P(\{\omega:\liminf_n X_n(\omega) < \limsup_n X_n(\omega)\}) \\ = \ & P(\cup_{a,b\in \mathbb{Q}}\{\omega:\liminf_n X_n(\omega) < a < b < \limsup_n X_n(\omega)\}) \\ \leq \ & \sum_{a,b\in \mathbb{Q}} P(\{\omega:\liminf_n X_n(\omega) < a < b < \limsup_n X_n(\omega)\}), \end{aligned} \tag{2.2.2}$$
而有理数是可列的;因此,要证明a.s.-收敛,只需证明对于任意一对满足$a < b$的有理数$a,b$,下式成立:
and rational numbers are countable; therefore, to prove the a.s. convergence, one only needs to prove that for any pair of rational numbers $a, b$ with $a < b$, the following holds:
$$P(\{\omega:\liminf_n X_n(\omega) < a < b < \limsup_n X_n(\omega)\}) = 0. \tag{2.2.3}$$
现在,考虑推论2.3.2所定义的上穿次数$U_n$。一方面,容易看出,式(2.2.3)中的事件对应$\{\omega:\lim_n U_n(\omega) = \infty\}$;另一方面,当$X_n$是一个下鞅时,根据推论2.3.2,有$EU_n \leq \frac{1}{b-a}[E(X_n - a)^+ - E(X_0 - a)^+]$。因此,在$X_n$进一步满足$\limsup_n EX_n^+ < \infty$时,有$\limsup_n EU_n \leq \frac{1}{b-a} \limsup_n (EX_n^+ + |a| - E(X_0 - a)^+) < \infty$;然后再通过$U_n$的单调递增性质,可用单调收敛定理证明$E\lim_nU_n = \limsup_n EU_n < \infty$,从而证明式(2.2.3)成立。总而言之:
Now, consider the upcrossing number $U_n$ defined in corollary 2.3.2. On the one hand, it is obvious that the event in equation (2.2.3) is equivalent to $\{\omega:\lim_n U_n(\omega) = \infty\}$; on the other hand, when $X_n$ is a submartingale, $EU_n \leq \frac{1}{b-a}[E(X_n - a)^+ - E(X_0 - a)^+]$ according to corollary 2.3.2. Therefore, if we further have $\limsup_n EX_n^+ < \infty$, we can show that $\limsup_n EU_n \leq \frac{1}{b-a} \limsup_n (EX_n^+ + |a| - E(X_0 - a)^+) < \infty$. Because $U_n$ increases monotonically w.r.t. $n$, we can apply the monotone convergence theorem to show that $E\lim_nU_n = \limsup_n EU_n < \infty$, which completes the proof of (2.2.3). In summary:
定理2.4:若下鞅$X_n$满足$\sup_n EX_n^+ < \infty$,则该下鞅a.s.-收敛到某个随机变量$X$。
Theorem 2.4: If $X_n$ is a submartingale with $\sup_n EX_n^+ < \infty$, then it a.s. converges to a random variable $X$.
(注:通过一些测度论中的收敛性定理,我们还可以进一步证明收敛到的$X$满足$E|X|<\infty$。)
(Note: We can further prove that $E|X|<\infty$ by applying some convergence theorems in measure theory.)
根据鞅的定义,容易证明对任意$n,m \in \mathbb{N}$,有$EX_n = EX_m$。而根据上面的讨论,在$X_n$满足一定正则性条件时,可以知道$X_n$几乎处处地逐点收敛到某个$X$。那么是否有$EX_n=EX$呢?遗憾的是,虽然a.s.-收敛是一个很强的性质,但不能够直接推导出上面这种收敛性;例如,考虑样本空间$\Omega=[0,1]$,并考虑$X_n(\omega) = nI(\omega \leq 1/n)$;容易看出虽然$X_n$ a.s.-收敛到$X = 0$,但$EX_n \equiv 1 \neq EX$。在该反例中,主要的问题在于:在$X_n\to X = 0$的过程中,虽然大偏差事件$\{|X_n-X| > \varepsilon \}$的测度在变小,但是相应的偏差值$|X_n-X|$在变大,使得整体偏差不收敛。在测度论中,可以通过引入“一致可积”这一条件来限制这类偏差的过快增长、从而避免上述问题;而在概率论中,同样可以考虑类似的条件。下面给出一种常见的定义:对于任意$\varepsilon > 0$,存在$M \in [0,\infty)$使得
From the definition of martingales, it is obvious that for any $n,m \in \mathbb{N}$, $EX_n = EX_m$. And, according to the above discussion, when $X_n$ satisfies certain regularity conditions, it will converge a.s. to some $X$. Can we now conclude $EX_n=EX$? Unfortunately, the answer is negative, even though the a.s. convergence is a very strong property. For example, consider sample space $\Omega=[0,1]$ and r.v. $X_n(\omega) = nI(\omega \leq 1/n)$; although $X_n$ converges a.s. to $X = 0$, we have $EX_n \equiv 1 \neq EX$. In this counterexample, the major problem is that: as $n$ increases, although the measure of the large deviation event $\{|X_n-X| > \varepsilon \}$ becomes smaller, the corresponding deviation $|X_n-X|$ is getting even larger, and their product does not converge to 0. To resolve this problem, in measure theory, people introduce the concept of “uniformly integrable” to bound the growth of extreme deviations. Similar conditions exist in the probability theory. A common definition is as follows: for any $\varepsilon > 0$, there exists an $M \in [0,\infty)$ such that
$$E(|X_n|I_{|X_n| > M}) < \varepsilon, \ \forall n \in \mathbb{N}. \tag{2.2.4}$$
容易检验上面反例中的$X_n$并不满足条件(2.2.4)。
It is easy to verify that the $X_n$ in the above counterexample do not satisfy condition (2.2.4).
若序列$X_n$满足(2.2.4)中定义的一致可积性,那么通过考虑使$E(|X_n|I_{|X_n| > M}) < 1, \ \forall n \in \mathbb{N}$成立的$M$,可知$E|X_n| < M+1 < \infty$,从而定理2.4中的条件$\sup_n EX_n^+ < \infty$成立。因此,若$X_n$同时是一个下鞅,则根据定理2.4可知$X_n$ a.s.-收敛到某个随机变量$X$。我们还可以进一步证明:
If a sequence $X_n$ is uniformly integrable as defined in (2.2.4), then there must be an $M>0$ such that $E(|X_n|I_{|X_n| > M}) < 1, \ \forall n \in \mathbb{N}$, so it is obvious that $E|X_n| < M+1 < \infty$, which leads to the condition $\sup_n EX_n^+ < \infty$ in theorem 2.4. Therefore, if $X_n$ is a submartingale, then according to theorem 2.4, $X_n$ converges a.s. to a random variable $X$. We can further show that:
定理2.5:若下鞅$X_n$满足一致可积性,则该下鞅按$L^1$收敛到$X$:
Theorem 2.5: If $X_n$ is a uniformly integrable submartingale, then it converges to some $X$ in $L^1$:
$$E|X_n - X| \to 0.$$
在这一小节的最后,我将介绍一些定理2.4和2.5的推论:
At the end of this subsection, I will introduce some corollaries from theorems 2.4 and 2.5:
推论2.5.1:若$\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$,$X\in \mathcal{F}_{\infty}$,$X\in L^1$,则$E(X|\mathcal{F}_n)$按a.s.和$L^1$收敛到$X$。该定理说明随着信息集变得丰富,对某个随机变量$X$的估计会变得更精细,最终收敛到$X$本身。
推论2.5.2(Levy 0-1律):若$\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$,$A\in \mathcal{F}_{\infty}$,则$E(1_A|\mathcal{F}_n) \to 1_A$ a.s.。该推论是推论2.5.1的一个直接应用。
推论2.5.3(条件期望的控制收敛定理):若$\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$,$Y_n \to Y$ a.s.,且存在$Z \in L^1$满足对任意$n \in \mathbb{N}$有$|Y_n| \leq Z$,则$E(Y_n|\mathcal{F}_n) \to E(Y|\mathcal{F}_{\infty})$ a.s.。
Corollary 2.5.1: If $\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$, $X\in \mathcal{F}_{\infty}$, $X \in L^1$, then $E(X|\mathcal{F}_n)$ converges to $X$ a.s. and in $L^1$. This theorem states that as one has more information, the estimate of the random variable $X$ will become more accurate and eventually converge to $X$.
Corollary 2.5.2 (Levy’s 0-1 law): If $\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$, $A\in \mathcal{F}_{ \infty}$, then $E(1_A|\mathcal{F}_n) \to 1_A$ a.s.. This corollary can be derived directly from corollary 2.5.1.
Theorem 2.5.3 (Dominated convergence theorem for conditional expectations): If $\mathcal{F}_n \uparrow \mathcal{F}_{\infty}$, $Y_n \to Y$ a.s., and there exists an $Z \in L^1$ that $|Y_n| \leq Z$ holds for any $n \in \mathbb{N}$, then $E(Y_n|\mathcal{F}_n) \to E(Y|\mathcal{F}_{\infty})$ a.s..
要证明推论2.5.3,注意到
To prove corollary 2.5.3, notice that
$$\limsup_n |E(Y_n - Y|\mathcal{F}_n)| \leq \limsup_n E(|Y_n - Y||\mathcal{F}_n) \leq \limsup_n E(W_N|\mathcal{F}_n) = E(W_N|\mathcal{F}_{\infty})$$
对任意$N$成立,其中$W_N \equiv \sup_{n,m \geq N} |Y_n - Y_m|$满足$W_N \downarrow 0$ a.s.。因此,$\limsup_n |E(Y_n - Y|\mathcal{F}_n)| = 0$ a.s.。结合上式和推论2.5.1即得证。
holds for any $N$, where $W_N \equiv \sup_{n,m \geq N} |Y_n - Y_m|$ and $W_N \downarrow 0$ a.s.. Therefore, $\limsup_n |E(Y_n - Y|\mathcal{F}_n)| = 0$ a.s.. The proof is completed once we combine this result with corollary 2.5.1.
可选停时定理 Optional Stopping Theorems
在这一小节中,我将讨论停时下的鞅$X_T$的性质。
In this subsection, I will discuss the properties of martingales that stop at random times $X_T$.
首先,若$X_n$是一个下鞅,$T$是一个停时,则根据推论2.3.1中推导,有$X_{T \wedge n} - X_0 = (1_{\{T\geq \cdot \}}\cdot X)_n$对任意$n \in \mathbb{N}$成立。又注意到$X_n - X_0 = (1 \cdot X)_n$,故可得
First, if $X_n$ is a submartingale and $T$ is a stopping time, then according to the corollary 2.3.1, $X_{T \wedge n} - X_0 = (1_{\{T\geq \cdot \}}\cdot X)_n$ for any $n \in \mathbb{N}$. Notice that $X_n - X_0 = (1 \cdot X)_n$; so we have
$$EX_0 \leq EX_{T \wedge n} \leq EX_n. \tag{2.3.1}$$
当$T$是一个a.s.-有界停时、且满足$P(T \leq n) = 1$的上界$n$已知时,可直接根据式(2.3.1)得到$EX_0 \leq EX_T \leq EX_n$。而当$T$可能无界时,需要对式(2.3.1)进一步取极限$n\to \infty$来得到关于$EX_T$的结果。根据上一小节对$L^1$收敛的讨论,为了保证$\lim_n EX_n$具有良好的性质,此时我们需要$X_n$满足一致可积性。又可以证明,在$X_n$是一致可积的情况下,$X_{T \wedge n}$也是一致可积的,从而$\lim_n EX_{T \wedge n}$也具有良好的性质。综合前述讨论可得以下结论:
When the stopping time $T$ is bounded a.s. and an integer upper bound $n$ (with $P(T \leq n) = 1$) is provided, we can derive from (2.3.1) directly that $EX_0 \leq EX_T \leq EX_n$. When $T$ may be unbounded, to obtain results about $EX_T$ we need to take limits $n\to \infty$ w.r.t. formula (2.3.1). According to the discussion of $L^1$ convergences in the previous subsection, in order to ensure that $\lim_n EX_n$ has good properties, we need $X_n$ to be uniformly integrable. However, it can further be shown that $X_{T \wedge n}$ is uniformly integrable when $X_n$ is so, and in this case, the limit $\lim_n EX_{T \wedge n}$ also has good properties. In summary, we have the following result:
定理2.6:若下鞅$X_n$满足一致可积性,则对任意停时$T$,下列不等式成立:
Theorem 2.6: If $X_n$ is a uniformly integrable submartingale, then for any stopping time $T$, the following inequality holds:
$$EX_0 \leq EX_T \leq E\lim_n X_n. \tag{2.3.1}$$
通过定理2.6可证得以下有用的推论:
The following useful corollary can be derived from theorem 2.6:
推论2.6.1(可选停时定理):若停时$L,M$满足$L \leq M$,且下鞅$X_{M \wedge n}$是一致可积的,则$EX_L \leq EX_M$且$X_L \leq E(X_M|\mathcal{F}_L)$。
Corollary 2.6.1 (optional stopping theorem): If $L \leq M$ are stopping times and $X_{M \wedge n}$ is a uniformly integrable submartingale, then $EX_L \leq EX_M$ and $X_L \leq E(X_M|\mathcal{F}_L)$.
换句话说,这个推论说明:在一致可积条件下,鞅在确定性时间$n$上的性质可以推广到停时$T$上。
In other words, this corollary says that under uniform integrability, the properties of martingales at deterministic times $n$ can be extended to any stopping time $T$.
应用 Applications
在这一节中,我将介绍一些鞅的应用。
In this section, I will introduce some applications of martingales.
首先,我们可以使用定理2.6和推论2.6.1来计算一些与停时相关的期望值。例如,考虑一个简单随机游走过程$S_n = X_1 + \cdots + X_n$,其中$X_i$是独立同分布的二项随机变量:$P(-1)=P(1)=0.5$。现在,假设给定一个整数$a > 0$,我们希望计算停时$T = \inf\{n:S_n \notin (-a,a)\}$的前几阶矩$ET,ET^2,\cdots$。由于$S_T \equiv a$,因此我们可以通过构造关于$S_n$和$n$的鞅来间接计算$T$的矩。例如,利用$S_n^2 - n$是鞅,可以得到$ET = ES_T^2 = a^2$;利用$S_n^4 - 6nS_n^2 + 3n^2 + 2n$是鞅,可知$ET^2 = \frac{1}{3}(6ETS_T^2 - ES_T^4 - 2ET) = \frac{1}{3}(6a^4 - a^4 - 2a^2) = \frac{5a^4 - 2a^2}{3}$。
First, we can use theorem 2.6 and corollary 2.6.1 to calculate some expectations w.r.t. stopping times. For example, let’s consider a simple random walk $S_n = X_1 + \cdots + X_n$, where $X_i$ are i.i.d. binomial random variables: $P(-1)=P(1)=0.5$. Now, suppose an integer $a > 0$ is given, and we want to calculate the first few moments $ET , ET^2, \cdots$ of the stopping time $T = \inf\{n:S_n \notin (-a,a)\}$. Since $S_T \equiv a$, we can implicitly calculate the moments of $T$ by constructing martingales with $S_n$ and $n$. For example, using the fact that $S_n^2 - n$ is a martingale, we have $ET = ES_T^2 = a^2$; using the fact that $S_n^4 - 6nS_n^2 + 3n^2 + 2n$ is a martingale, we have $ET^2 = \frac{1}{3}(6ETS_T^2 - ES_T^4 - 2ET) = \frac{1}{3}(6a^4 - a^4 - 2a^2) = \frac{5a^4 - 2a^2}{3}$.
其次,由于在鞅的定义中只对期望值作出了要求,因此与鞅相关的大偏差估计和集中不等式可以应用到更广泛的场景中。例如,Azuma不等式作为Hoeffding不等式在鞅上的推广,被用于许多随机算法的设计及收敛速度分析中。Azuma不等式的详细证明可以参考以下课件,此处不再赘述。在这里,我想仔细介绍另一个有意思的结果:Doob不等式。该不等式说明了一个鞅序列中的极大偏差可以被该序列最后一项控制;因此,通过该不等式,一些关于鞅序列全体的极值估计可以通过分析尾项来实现。
Secondly, because in the definition of martingales only conditions on expectations are required, large-deviation estimates and concentration inequalities for martingales can be applied to more general scenarios. For example, as a generalization of Hoeffding’s inequality to martingales, Azuma Inequality is used in the design and the analysis of convergence rates of many non-deterministic algorithms. Readers interested in the detailed proof of Azuma’s inequality can refer to the following lecture notes. Here, I want to introduce another interesting result: Doob’s inequality. This inequality says that the maximum deviation in a martingale can be controlled by its last term; therefore, with this inequality, one can provide some large-deviation estimates of the martingale simply by analyzing the last term.
定理3.1:假设$X_n$是一个下鞅,且常数$\lambda > 0$。若考虑极值$\bar{X}_n = \max_{0\leq m\leq n} X_m^+$,事件$A = \{\bar{X}_n \geq \lambda\}$,及停时$T = \inf\{m:X_m \geq \lambda \text{ or } m = n\}$,则可得下列结果
Theorem 3.1: Suppose $X_n$ is a submartingale and we are given a constant $\lambda > 0$. Consider the extreme value $\bar{X}_n = \max_{0\leq m\leq n} X_m^+$, the event $A = \{\bar{X}_n \geq \lambda\}$, and the stopping time $T = \inf\{m:X_m \geq \lambda \text{ or } m = n\}$. Then we have
$$\lambda P(A) \leq EX_T1_A \leq EX_n1_A \leq EX_n^+1_A \leq EX_n^+.$$
其中,第一个不等式成立是因为在$A$上$X_T \geq \lambda$;第二个不等式成立是因为定理2.6指出$EX_T \leq EX_n$,且在$A^c$上$T=n$;最后两个不等式成立是显然的。
In above, the first inequality holds because $X_T \geq \lambda$ on $A$; the second inequality holds because theorem 2.6 implies that $EX_T \leq EX_n$ and $T=n$ on $A^c$; and the last two inequalities are trivial.