随着数据收集能力的提升和控制手段的复杂化,在实际业务中,常常会遇到对多维、异质化的处置效应(treatment effect)的估计问题。近年来,学界在这个方向上提出了一些新的方法和工具;其中一个较为知名的工作是Susan Athey等人提出的generalized random forest(grf)。不过,这些工具与当前业界常用的工具(例如XGBoost,下称为xgb)存在一定差距:
- 未针对大规模数据场景进行计算效率优化,训练和推断时间较长;
- 功能局限于少数几种场景,无法支持多样化的建模需求;
- 设计时主要考虑离线分析场景,缺乏对线上部署等工程应用场景的原生支持。
考虑到这些痛点,在这一篇文章中,我将基于对这些新估计方法的认识和对xgb等常用工具的理解,提出(或者是重新发现)数种处置效应估计方法,以尝试结合xgb的计算效率和新方法的估计准确性。然后,我将通过一系列简单的数值实验,对这些方法在估计准确性、计算效率和开发效率等各方面的优劣进行评估。最后,我将根据这些实验结果和个人经验,对这些方法的实际使用给出一些个人建议。
问题定义
假设在一组处理变量$X_t$和结果(outcome) $y$之间,存在一种参数化关系$y = f(X_t|\theta)$,其中结构化形式$f$已知,而参数$\theta$未知,但可能与另外一些可观测的(observable)控制变量$X_s$存在关联;不妨用非参数映射$\theta=g(X_s)$表示这种关系。现在,给定一组数据$D=\{(X_{s,i},X_{t,i},y_i)\}_{1 \leq i \leq N}$,我们希望能够根据这组数据找到一个好的映射$g$。具体做法可以是最小化某种经验损失函数$L(g|D)$,例如关于$y$的损失函数$\mathbb{E}_{D} L_y(y,f(X_t|g(X_s)))$。
例如,在商品定价场景中,如果$y$表示(相对)需求量,$X_t$表示(相对)价格,那么$f$可以表示一种弹性关系:$\ln(y) = \theta \cdot \ln(X_t)$。根据经验,需求弹性$\theta$通常会受到季节、是否周末、是否节假日等外生变量的影响;而我们的目标即通过历史数据$D$,建立这些变量$X_s$与需求弹性$\theta$之间的关系。
在这类问题中,相比结果$y$,我们通常更关心参数$\theta$的估计准确性(数值准确性或者排序一致性)。例如,在上述定价场景中,我们较为关注的业务问题可能是“在哪些时段进行打折促销会有更好的刺激效果”;此时,对不同时段的弹性的排序准确度相比对需求量估计的准确度要更为重要。
注:在上述问题定义中,模型同时包含了结构化部分$f$和非结构化部分$g$,因此该问题可以认为是一种半结构化建模(semi-structural modeling)任务。
估计方法
xgb + 局部回归 (local regression)
一种简单直接的估计方式,是先根据损失$L_y$,通过xgb等非参数模型拟合$\tilde{f}(X_s,X_t)$ $$
\tilde{f} = \arg\min_{\tilde{f}} \mathbb{E}_{D} L_y( y,\tilde{f}(X_s,X_t) ), $$ 然后(在推断阶段)通过局部回归的方式获取$g$:对每个确定的控制变量$X_s$,我们令相应的参数估计$\hat{\theta}$为 $$
\hat{\theta}(X_s) = \arg\min_{\theta} \sum_k L_y( \tilde{f}(X_s,X_{t,k}),f(X_{t,k}|\theta) ), $$ 其中$X_{t,k}$是一组采样得到的处理变量。
这种方法的好处在于可以直接沿用现有的建模工具,增量开发成本低;但其存在以下缺点:
- 参数估计阶段计算量大:当$X_t$维度较高时,需要较多的采样样本才能使$\theta$的估计值收敛到合理水平;
- 参数估计准确率低:第二阶段估计容易受到第一阶段模型$\tilde{f}$中噪声的影响,导致误差累积。
grf
grf由Susan Athey, Julie Tibshirani, Stefan Wager等人于2016年提出,是一种基于随机森林(random forest,下记为rf)的参数估计方法。其与传统的随机森林算法的主要区别在于以下两点:
- (split for heterogeneity) 调整了树的分裂标准,以更强调不同分支间参数的差异性。具体来说,在一次分裂过程中,给定样本集合$D$和全局参数估计值$\theta_D$,如果假设样本$i$对于$\theta_D$的局部贡献程度可用变量$\rho_i$表示:$$
\theta_{D’} \approx \theta_D + \sum_{j \in D’} \rho_j; $$ 那么这次分裂的目标是找到一种$D$的切分方法$(D_1,D_2)$,以最大化切分后两部分平均$\rho$的差异程度 $$
\max \frac{1}{|D_1|} (\sum_{j\in D_1} \rho_j)^2 + \frac{1}{|D_2|} (\sum_{j\in D_2} \rho_j)^2. $$ $\rho_i$的具体取值可以按以下方式确定:首先,我们将$\rho_i$定义为$\theta_{D \cup \{i\}} - \theta_{D}$。然后,注意到在理想情况下,条件$\sum_{j \in D’}g_j(\theta_D’) = 0$应对任意样本集合$D’$成立,因此有 $$
\begin{aligned}
0 & = \sum_{j \in D \cup \{i\}} g_j(\theta_{D \cup \{i\}}) = \sum_{j \in D} g_j(\theta_D + \rho_i) + g_i(\theta_D + \rho_i) \\
& \approx \sum_{j \in D} [g_j(\theta_D) + \rho_i\cdot h_j(\theta_D)] + g_i(\theta_D) = \rho_i \cdot \sum_{j \in D} h_j(\theta_D) + g_i(\theta_D),
\end{aligned} $$ 即$\rho_i \approx (\sum_{j \in D} h_j(\theta_D))^{-1} g_i(\theta_D)$. - (honesty) 树的分裂和叶子结点赋值分别采用了一组独立样本,以减轻过拟合风险。
算法的详细思路和实现逻辑可以参考相应的论文和工具包的介绍页面。另外,目前grf工具包只能支持一维参数估计,对于多维处置效应的估计,可以参考其扩展mgrf。
相比上面xgb+局部回归的方案,grf的优点在于有较优的理论性质,但其缺点也很明显:
- 首先,grf主要基于rf,在数据量充足时,估计准确度要差于基于boosting的xgb;
- 为了提高估计准确度,grf提高了重新近似的频率以降低近似误差:grf在结点维度进行近似,而xgb只在树维度进行近似。这导致在构建单颗树时,grf的计算量要更大。
- 最后,由于grf工具包的调用API是基于R的,不便于多语言调用,导致工具缺乏关注度和社区维护,发展较为缓慢,对工程应用场景的支持较差。
mbst (multivariate booster)
xgb可以看作是一种一维参数估计方法(考虑控制变量$X_t$为常数1、作用函数$f(X_t|\theta) = \theta$的情况);因此可以尝试将其估计思路推广到高维场景中。xgb的基础模型是提升树(boosted tree):在每一轮次中,生成新的树对此前的预测结果进行修正;最终的预测结果为各轮次树的预测结果的线性叠加。相对于传统的提升树方法,xgb通过对损失函数$L(\theta)=L_y(y,f(X_t|\theta))$进行二阶泰勒展开来降低计算量。具体来说,假设在第$n$轮提升后,样本$i$对应的参数估计值为$\theta_{n,i}(X_{s,i})$,那么有 $$
L(\theta_{n+1,i}) \approx L(\theta_{n,i}) + g_i \cdot d\theta_{n+1,i} + \frac{1}{2} h_i \cdot d\theta_{n+1,i}^2; $$ 其中$g_{n,i},h_{n,i}$分别代表$\nabla L(\theta_{n,i}), \nabla^2 L(\theta_{n,i})$。基于此展开形式,对于一组样本$D$,最优的参数修正量$d\theta_{n+1,D}$可以通过求解二次函数极值点得到:$$
d\theta_{n+1,D} = \frac{\sum_{i \in D} g_{n,i}}{\sum_{i \in D}h_{n,i} + \lambda}, $$ 其中$\lambda$是一个正则项。根据上述表达式可以进一步完成分裂步骤(选取增益值最大的分裂选项)和赋值步骤(对每个叶子结点计算相应的$d\theta$)的算法设计。
在多维场景中,二阶泰勒展开的形式变为 $$
L(\theta_{n+1,i}) \approx L(\theta_{n,i}) + g_i^T \cdot d\theta_{n+1,i} + \frac{1}{2} d\theta_{n+1,i}^T \cdot h_i \cdot d\theta_{n+1,i}; $$ 因此样本集合$D$所对应的参数修正量$d\theta_{n+1,D}$可以通过一次ridge regression获得:$$
d\theta_{n+1,D} = (\sum_{i \in D}h_{n,i} + \lambda I)^{-1} (\sum_{i \in D} g_{n,i}). $$ 我将上述这种估计方法称为mbst(multivariate booster的简写)。该方法的优点在于算法思路简单,可以直接对多维、异质性参数进行估计,易于根据不同的需求场景进行定制化(例如支持不同的损失函数$L$)。不过,目前,xgb的实现是基于一维参数估计的,若按上述方法拓展到多维场景会有较大的改动量(具体来说,目前梯度$g$和Hessian矩阵$h$等变量都用float类型存储;如果要支持多维参数估计,则需要将类型改为Vector或者类似类型),开发成本较高,因此在实际使用上存在一定障碍。
多阶段(multi-stage) xgb
当处理变量$X_t$和作用函数$f$具有特殊形式$X_t=(1,w), f(X_t|\theta) = \theta_0 + \theta_1 w$时(即结果可线性分解为基础效应+一维处置效应),一种常用的估计方法是进行两阶段估计:首先,根据损失函数$L_y(y,\tilde{f}_y(X_s))$和$L_w(w,\tilde{f}_w(X_s))$分别建立关于$y$和$w$的预测模型$\tilde{f}_y(X_s)$和$\tilde{f}_w(X_s)$;然后,定义新的预测目标$\tilde{\theta}_{1} = (y - \tilde{f}_y(X_s))/(w - \tilde{f}_w(X_s))$,并根据损失函数$L_{\theta}(\tilde{\theta}_1,\tilde{g}(X_s))$建立关于$\theta_1$的非参数预测模型。最终,通过下式给出完整的参数估计:$$
\hat{\theta}(X_s) = (\tilde{f}_y(X_s) - \tilde{f}_w(X_s) \cdot \tilde{g}(X_s),\tilde{g}(X_s)). $$ 这种估计方法的好处在于,上述两阶段建模都可以沿用现有工具,因此增量开发成本很小。在grf对一维处置效应的估计(即causal forest)中,也采用了这种方法。
通过一些技术处理,上述两阶段思路可以拓展到多维(线性)处置效应场景。具体来说,在第一阶段先建立$y$和$X_t$的预测模型,用于去除偏差(debias);然后,在第二阶段遍历各处理变量$X_t$,拟合其与$y$之间的相关关系(即估计相应的$\theta$)。这种做法类似于优化中的坐标下降法:每次选择一个参数进行估计,估计时固定其他n-1个参数。不过,上述拓展方法有以下两个明显的缺点:
- 当各处理变量$X_t$之间存在自相关性时,估计结果很可能有偏。而且,$X_t$的遍历顺序可能会对不同位置的参数估计的相对准确度有影响,降低估计结果的稳定性。
- 计算量随着处理变量$X_t$的数量线性增长:通常,需要建立$m+1$个基础模型(用于去除偏差)和$m$个处置效应模型,其中$m$是处理变量$X_t$的数量。
因此,在实践中,这种方法主要还是用于前述两阶段场景(结果可线性分解为基础效应+一维处置效应)中。
投影(projected) mbst
最后,我们考虑另一种利用现有工具进行多维参数估计的思路:
- 首先,在计算量最密集的分裂阶段,通过投影近似的方法将多维梯度和Hessian矩阵信息转化为一维信息,然后调用xgb这种高效的分裂器(efficient split finder)生成树的结构。具体来说,在投影时,先将多维梯度$g$和Hessian矩阵$h$按某个平均修正量$\mu_{d\theta}$进行平移,然后沿某个投影方向$\sigma_{d\theta}$进行投影,得到一维梯度$g_{proj}$和Hessian值$h_{proj}$ $$ g_{proj} = \sigma_{d\theta}^T \cdot (g + h \cdot \mu_{d\theta}); \ h_{proj} = \sigma_{d\theta}^T \cdot h \cdot \sigma_{d\theta}; $$
- 然后,在计算量较少的赋值阶段,再通过mbst的思路,利用完整的多维信息来更新叶子结点的预测值,减轻分裂阶段的近似所带来的误差、提升估计准确度。
投影阶段的参数$\mu_{d\theta}$和$\sigma_{d\theta}$可按以下方式确定:
- $\mu_{d\theta}$可以取为样本平均修正量$(\sum_{i\in D} h_i + \lambda I)^{-1}(\sum_{i\in D} g_i)$;
- $\sigma_{d\theta}$的选取可以考虑以下几种方案:
- 选取使得投影后梯度$g_{proj}$波动性最大的方向作为投影方向。这种思路对应的直觉是,波动性越大通常意味着差异性越大,通过分裂能取得的增益越高。对波动性最大方向的求解可以通过对样本梯度矩阵$g$进行一维PCA实现,因此计算开销很小,是计算可行的。
- 由于二阶信息的存在,梯度方向和参数更新方向很可能不一致;如果能够将二阶信息考虑在内,可能可以获得质量更高的投影方向。但由于样本维度的二阶信息噪声较大,通常无法直接进行样本维度的方向修正(即$g_i \to h_i^{-1} g_i$),因此需要考虑一些近似方法。一种简单的思路是参考grf中的做法,考虑$\tilde{g} = (\sum_{i\in D} h_i)^{-1}g_i$。
- 另一种利用二阶信息的思路是借鉴一阶优化中动量的思路,通过在当前梯度方向中引入过往几次参数更新方向的信息,作为对新的参数更新方向的估计。这里,我将参考NAG(Nesterov Accelerate Gradient)的做法,先按照上一次参数更新方向$d\theta_{n-1}$进行外插$$\tilde{\theta}_n = \theta_n + lr \cdot \beta \cdot d\theta_{n-1},$$然后令潜在参数更新方向$\tilde{g}$为$$ \tilde{g} = g(\tilde{\theta}_n) + \beta \cdot d\theta_{n-1},$$其中$\beta \in [0,1]$是一个可调的超参数;
- 最后,可以参照数值计算中预估-校正的思路,先按照某个初始投影方向得到一颗树,然后选取使得这棵树各叶子结点$D_j$的预测修正量的投影$\sigma_{d\theta}^T (d\theta_{D_j} - \bar{d\theta}_D)$波动性最大的方向作为新的投影方向。该投影方向能够大致反映这轮boosting所倾向产生差异性的方向,因此较前几种方案要更有利于找到好的分裂选项。不过,这意味着每一轮boosting需要建两棵树,计算量增长了一倍。
数值实验
我们考虑以下实验方案:
- (生成数据集)先指定一组真实的映射关系$(f_{real},g_{real})$,然后将这组映射应用在一个输入变量数据集$(X_{s,i},X_{t,i})_{1\leq i \leq N}$上,得到相应的参数和结果$(\theta_{i},y_i)_{1\leq i \leq N}$,从而构成数据集$D$。具体来说,处理变量$X_t$和控制变量$X_s$都通过标准正态分布生成,但如果考虑基础效应(baseline effect),则处理变量$X_t$的第一维设置为常数1;$g_{real}(X_s)$通过一个mbst来表示,其中每棵树有固定深度,其每个结点的分裂方式和预测值都根据$X_s$随机生成,但预测值$\theta$不同维度的相对大小可以进行手动调整;$f_{real}(X_t|\theta)$则采用线性函数$\theta^T X_t$。
- (进行估计)然后,对数据集$D$应用前述各种估计方法,得到估计$(\hat{\theta}_{i},\hat{y}_i)_{1\leq i \leq N}$;
- (评估结果)最后,对估计结果进行评估。对于结果(outcome) $y$,我们考虑RMSE$\varepsilon_{y} = \frac{1}{N}\sum_i(y_i - \hat{y}_i)^2$;对于参数$\theta$,我们考虑RMSE$\varepsilon_{\theta} = \frac{1}{N}\sum_i(\theta_i - \hat{\theta}_i)^2$和Pearson相关系数$\rho_{\theta} = \rho(\theta,\hat{\theta})$。
注:$X_t$通过标准正态分布生成的好处是其均值为0,因此在多阶段xgb和grf中可以避免去除偏差(debias),从而节省部分计算量。
下面,我们分具体实验来讨论评估结果。不同实验间的主要差别在于处理变量$X_t$的个数、形式以及相对量级;而控制变量$X_s$和映射关系$g$的生成方式保持不变。结果表格中,除了明显能够对应到上述方法的列,mean baseline表示用样本均值$\bar{y}$和$\bar{\theta}$作为估计结果的基线水平;各投影mbst中,第一个字符(n/pc)对应是否进行预估-校正;第二个字符(n/c)对应是否进行中心化$\mu_{d\theta}$;第三个字符(g/hg/nag)则分别对应使用梯度、二阶修正、以及NAG来选取投影方向。
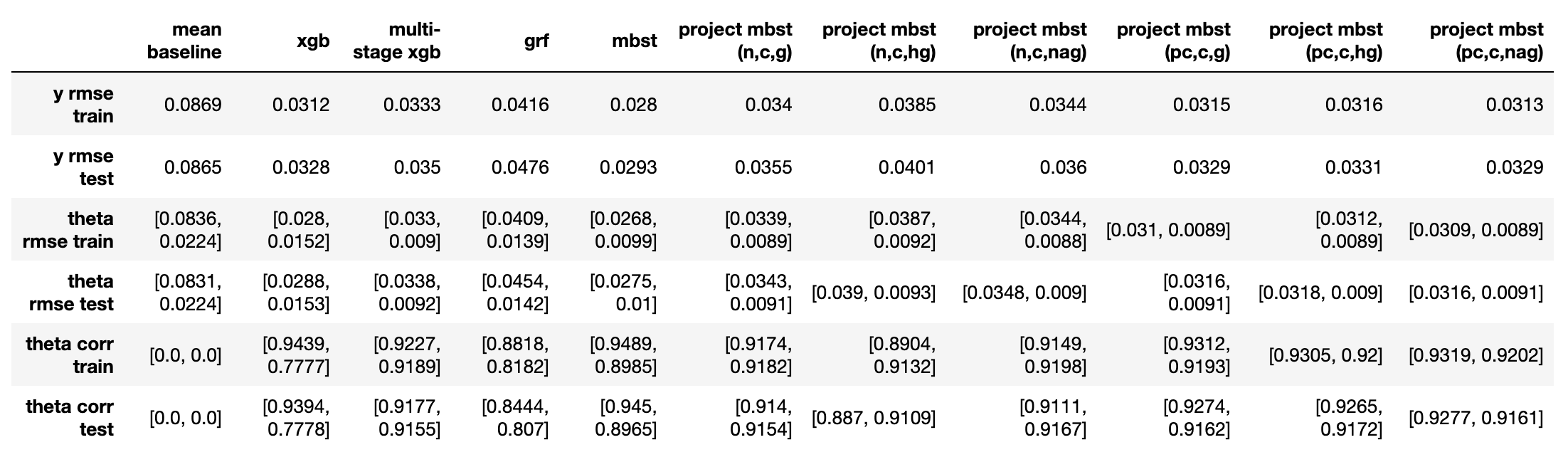
实验1:1倍基础效应+0.25倍处置效应
本实验主要观察在处置效应相比基础效应量级较小时,各方法能否准确捕捉到处置效应。
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst = xgb < 投影mbst = 多阶段xgb < grf;
- 而从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,各种投影mbst表现相似,与多阶段xgb一同表现最好,而mbst稍差一些;grf和xgb表现最差。
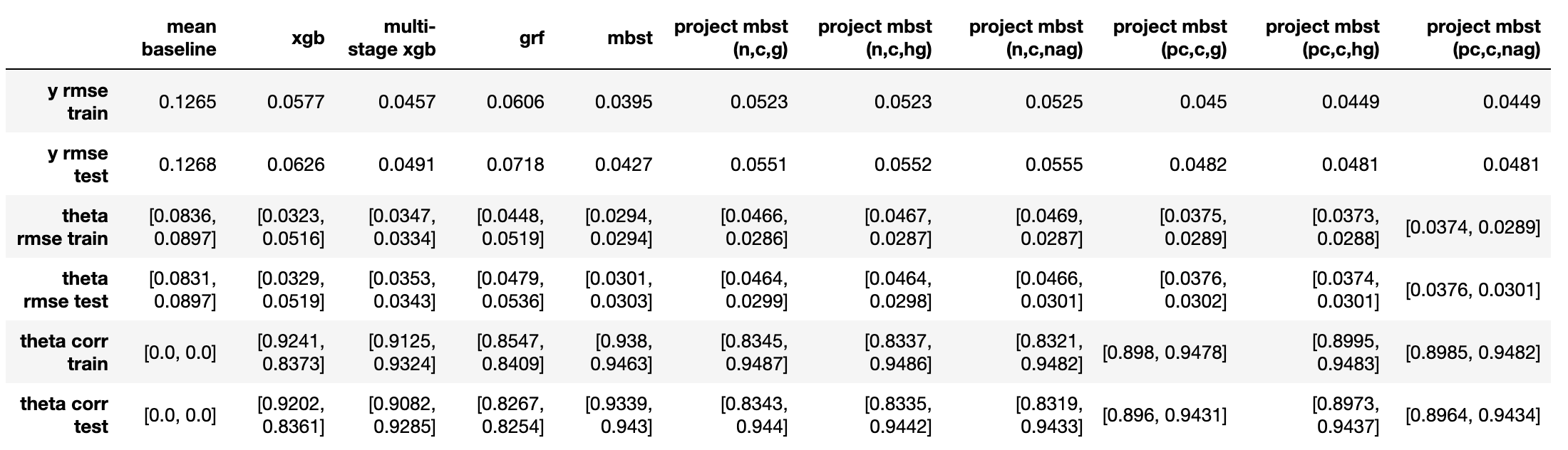
实验2:1倍基础效应+1倍处置效应
本实验主要观察当处置效应与基础效应量级相似时,各方法在预测最终结果$y$上的表现。
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst = 多阶段xgb < 投影mbst < xgb < grf;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,各种投影mbst表现相似,与mbst一同表现最好,而多阶段xgb稍差一些;grf和xgb表现最差。
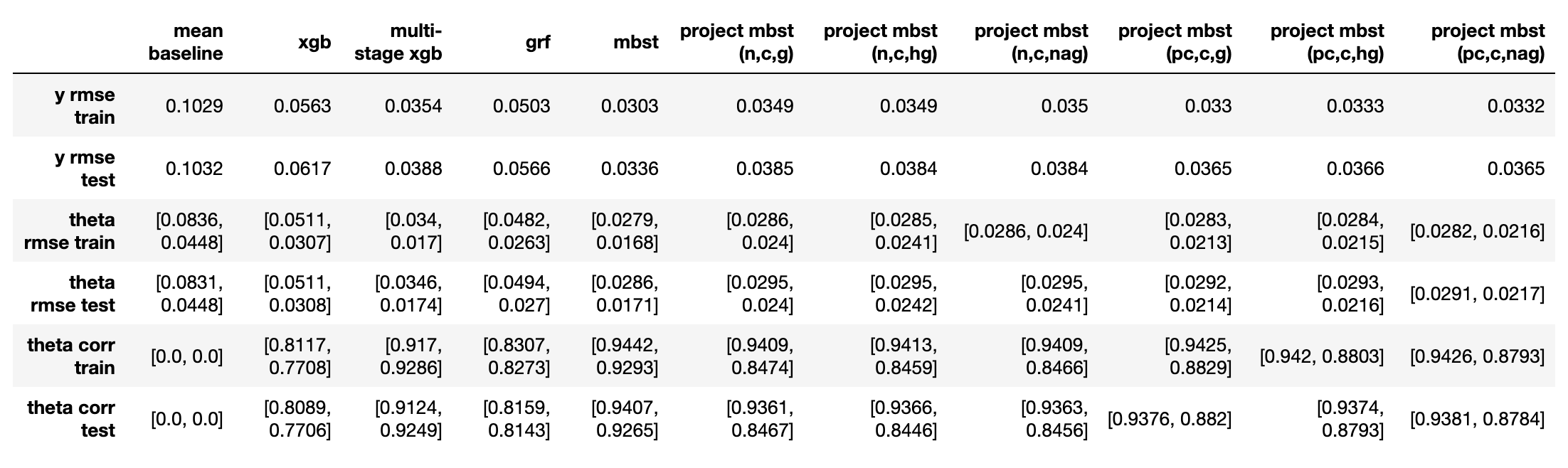
实验3:1倍处置效应(1)+0.5倍处置效应(2)
本实验主要观察当存在多个影响效果不同的处置效应时,各方法在各处置效应上的表现。
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst < 投影mbst = 多阶段xgb < grf < xgb;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,
- mbst在两个处置效应上表现都最好;
- 各种投影mbst在第一个(较大的)处置效应上表现相似,与mbst持平,校正方法主要在第二个(较小的)处置效应上有所提升;不同投影方向选取方法间没有明显区别;
- 多阶段xgb反而在第二个处置效应上效果与mbst持平,而在第一个处置效应上略差于各投影mbst;
- grf和xgb依然表现最差;故后续不再进行讨论。
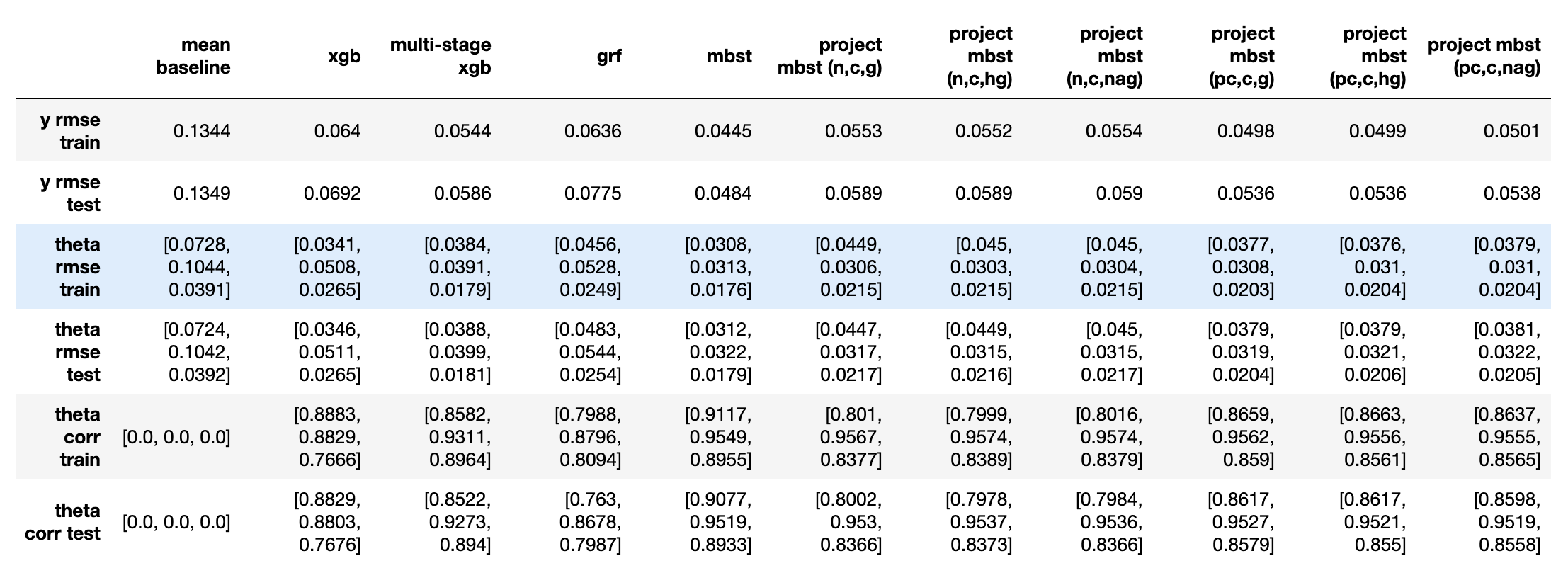
实验4:1倍基础效应+1倍处置效应(1)+0.5倍处置效应(2)
从本实验开始,后续实验都是作为前三个实验的延伸,进一步观察不同效应组合下各方法表现的相对好坏以及规律。
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst < 投影mbst = 多阶段xgb < grf < xgb;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,
- mbst在两个处置效应上表现都最好;
- 各种投影mbst在第一个(较大的)处置效应上表现相似,与mbst持平,校正方法主要在第二个(较小的)处置效应上有所提升;不同投影方向选取方法间没有明显区别;
- 多阶段xgb反而在第二个处置效应上效果与mbst持平,而在第一个处置效应上略差于各投影mbst。
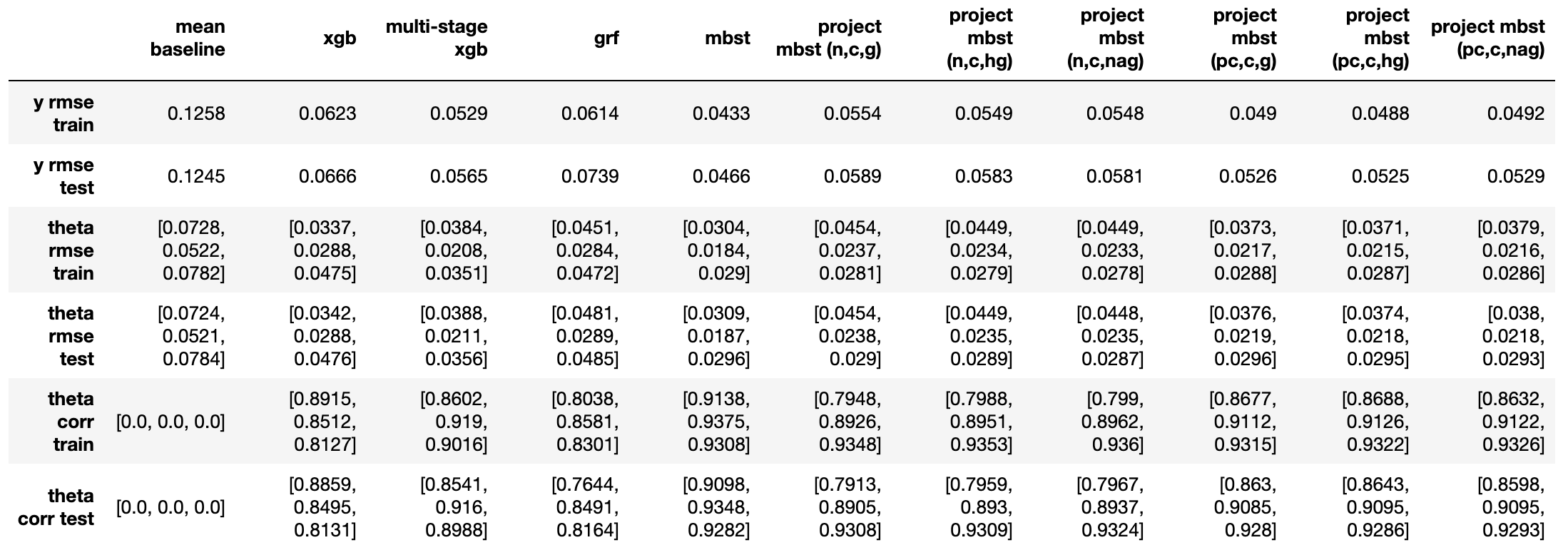
实验5:1倍基础效应+0.5倍处置效应(1)+1倍处置效应(2)
本实验的处置效应设计与实验4的处置效应正好量级相反。
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst < 多阶段xgb < 投影mbst < grf < xgb;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,
- mbst仍然在两个处置效应上表现都最好,后续不再讨论;
- 各种投影mbst在第二个(较大的)处置效应上表现相似,与mbst持平,校正方法主要在第一个(较小的)处置效应上有所提升;不同投影方向选取方法间没有明显区别;
- 多阶段xgb在两个处置效应上都差于mbst,但在在第一个处置效应上略好于各投影mbst。
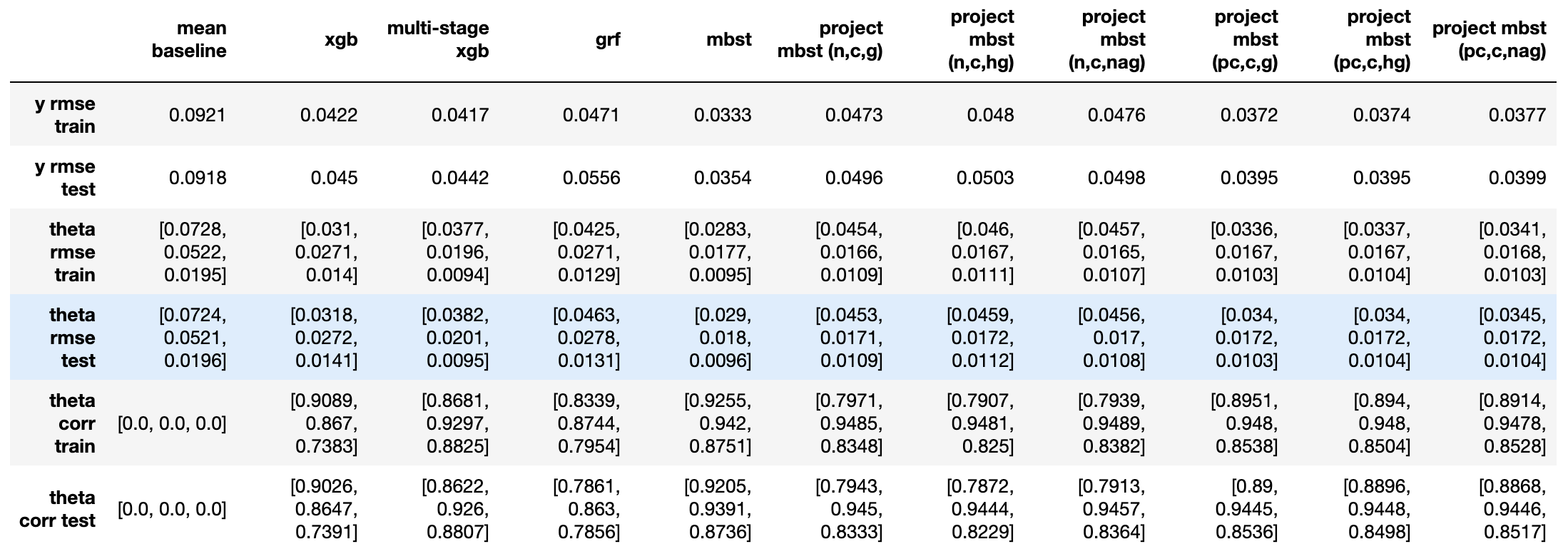
实验6:1倍基础效应+0.5倍处置效应(1)+0.25倍处置效应(2)
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst < 多阶段xgb < 投影mbst < grf < xgb;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,
- 各种投影mbst在第一个(较大的)处置效应上表现相似,与mbst持平,校正方法主要在第二个(较小的)处置效应上有所提升;不同投影方向选取方法间没有明显区别;
- 多阶段xgb反而在第二个处置效应上效果与mbst持平,而在第一个处置效应上略差于各投影mbst。
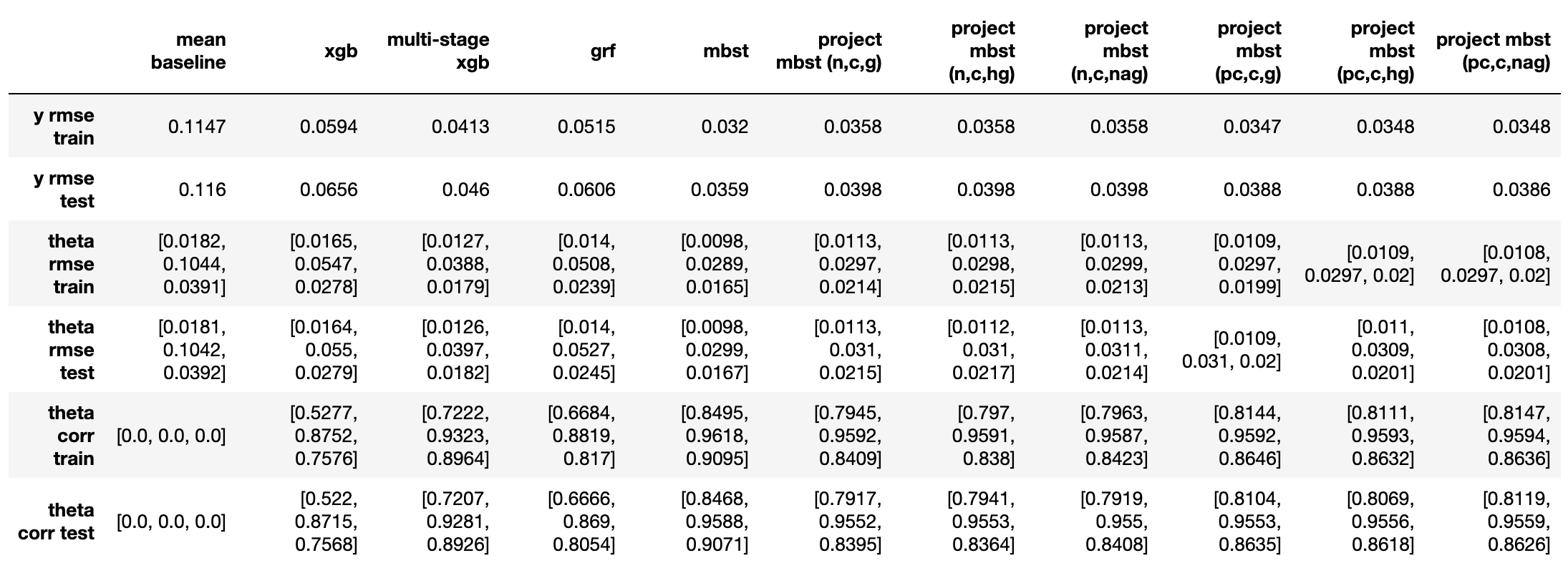
实验7:0.25倍处置效应(1)+1倍处置效应(2)+0.5倍处置效应(3)
- 从$\varepsilon_y$来看(越小代表越好,下同),mbst < 校正后投影mbst < 投影mbst < 多阶段xgb < grf < xgb;
- 从处置效应对应的$\varepsilon_{\theta}$和$\rho_{\theta}$来看,
- 各种投影mbst在第二个(较大的)处置效应上表现相似,与mbst持平,校正方法主要在其他两个(较小的)处置效应上有所提升;不同投影方向选取方法间没有明显区别;
- 多阶段xgb反而在第三个处置效应上效果与mbst持平,略好于各投影mbst;在第二个处置效应上略差于各投影mbst,在第一个处置效应上献出差于各投影mbst。
结论
根据上述实验可以看出,至少对于所测试的场景:
- mbst的表现一致最好,因此在计算和开发成本可以接受的情况下,尽量选用mbst;
- 当计算和开发成本较高时,投影mbst和多阶段xgb是两种有竞争力的备选方案。其中,投影mbst在估计效果上表现更优,通常能在最显著的单个处置效应上与mbst效果持平;而多阶段xgb则更易于开发、计算成本更低,整体估计效果也不错,但在不同处置效应上的表现受到执行顺序的影响,可能是实际应用中的一个风险点;
- grf的表现一致差于上述方法,一个可能的原因在于其基础模型是rf,通常bias更高;在处置效应估计方面,它还是好于xgb+局部回归的;
- xgb+局部回归并不适用于估计处置效应,应尽量避免使用。
具体的实验细节可以通过这个github repo获取;感兴趣的读者可以进一步开展其他评估实验。该repo同时提供了基于python和xgb的mbst和投影mbst的实现,读者可以在自己的数据集上校核其估计效果。
最后,我想从实际应用的角度,简单谈一谈mbst的局限性与应用方向。其实,提出mbst和投影mbst的初衷在于,常用树模型xgb较难直接或简单修改应用在处置效应的估计中,确实存在对新方法和工具的需求。然而,这些困难在神经网络(nn)上并不存在:现有的自动微分框架(tf、pytorch)可以直接支持建立半结构化模型、并进行定制化训练。因此,如果数据量足够充足,nn相比xgb有足够的统治性(dominant)时,可以直接考虑nn中的半结构化模型,无需使用mbst。但根据个人观察,实际应用中确实存在一些场景,在基础效应上数据充足,但在处置效应上数据较为稀疏。此时bias-variance tradeoff中的variance的重要度更高,在处置效应上树模型可能更实用;这时上述估计方法可能就能派上用场。
注:最后指出一个有趣的关联:在多年前,我曾经就choice modeling课中Quebec Energy Consumption这个case写过一篇文章,指出该数据集中可能存在类别划分(latent classes),并尝试通过树模型对这些类别进行挖掘、从而提升估计效果。这一工作可以看做是这篇文章中提到的估计方法的一个特殊应用,但在建模动机(motivation)上并不完全一致。